One of the most significant changes introduced in SAP 2009 was that affecting non-repeating thermal bridging.
The full effect of the change is only now being felt as more and more applications are drawn into the new regulations. Most schemes we work on will require some time and attention looking at Thermal Bridging.
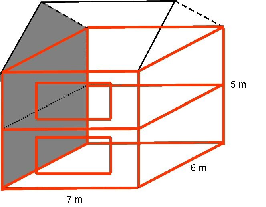
Figure 1: For a semi detached house with loft insulation, the lengths of red junctions would need to be measured to calculate the non repeating bridging heat loss – note this includes heat loss at the party wall
What is a Thermal Bridge?
Thermal Bridging refers to junctions between building elements and insulating materials which create a ‘weak link’, thus having a negative effect on the thermal performance of the building. There are three types of thermal bridges:
- Repeating thermal bridges such as timber studs in timber frame walls, or mortar joints in lightweight blocks. These are included in orthodox U Value calculations
- Non-repeating thermal bridges occur at joints between elements and around openings. These are accounted for in a SAP assessment by entering a calculated or default ‘y’ value
- Random thermal bridges occur where extra pieces of structure bridge the insulation layer.
An example would be a steel beam in a wall construction. Since steel is 2000 times more conductive than the best insulation, these can be very significant. The designer should make sure that these type of bridges are eliminated, but they are not included in the SAP calculations
Figure 2: The concentration of heat flux at the corner is often exacerbated by additional conductive materials.
In the previous version of SAP that we assessors have been using for some years (SAP 2005) it is possible to assess the impact of non-repeating thermal bridges very simply by simply stating that Accredited Construction Details have been adopted – and assigning a ‘y’ value of 0.08 W/m2K per °C to the entire dwelling, rather than calculating for each individual junction or bridge.
Whats a y-value?
The Y value can be thought of as an additional heat loss – averaged over the total heat loss area. For example, if you have an average fabric U-value of 0.3 W/m2K and a y-value of 0.08 the effect of the non-repeating thermal bridge would be to increase the U-value to 0.38W/m2K.
Whats a Psi (Ψ) value?
You’ll see reference to Psi values here also. You cant get a y – value without knowing the Ψ value. It is a measure of heat loss per K for every meter length of the junction – W/mK. Accredited Details have default maximum Ψ values covering the most common junctions as per table K1.
A New Approach to Thermal Bridging
Studies have shown that in practice, this simplified approach does not appear to be delivering buildings on the ground with the claimed thermal performance. A better approach is to assess the heat losses through each thermal bridge and to add them all up.
This approach was already available in SAP 2005, but it requires more work than being able to select a single ‘y value’ as previously mentioned.
As U-values are increasingly reduced to generate further CO2 reductions, the proportion of heat loss through thermal bridges becomes increasingly important. The only default ‘y value’ option now available in SAP 2009 is the worse case value of 0.15.
This in effect means that to use the default figure significantly increases the heat loss of the dwelling, and reduces the performance as far as SAP is concerned.
In order to overcome this, developers and SAP assessors will now need to examine the detailing at junctions, e.g. between walls, floors, roofs, windows and internal walls – and to properly assess the heat loss through thermal bridges. For this Psi values need to be known – you can get these from either:
- A suitably qualified person who will calculate the Ψ value for individual junctions or;
- Use Psi values as quoted by Accredited Construction Details – as long as ACD’s have been adopted for that junction
Changes in the SAP methodology for carrying out these calculations also mean that the calculated thermal bridging heat loss may be significantly higher in SAP 2009 than was the same calculation in SAP 2005. This is because SAP 2005 ignored junctions with party walls and, where Accredited Construction Details are not being used, the calculated values are also multiplied by 1.25. The calculated y value of a given dwelling type can be used in other dwellings of the same type.
Sounds complicated – what do I need to do?
In practice, every new build subject to Part L 2010 should as a minimum be using Accredited Construction Details – take a look at the website to familiarise yourself with the differing constructions and junctions. Your SAP assessor will need to know which details you are using so that he or she can adjust the calculations accordingly, and take the relevant figures from table K1.
You will then need to print each detail from the website and sign them – the assessor will need this evidence on completion. You may also use Enhanced Construction Details for greater gains. Other schemes are coming along also so watch this space.
ALTERNATIVELY – have the individual Psi values calculated by a suitably qualified person. Send these to your assessor who will manually input these into SAP. The assessor will need confirmation that this person is indeed suitably qualified.
Read our updated Blog for a view on ACDs in SAP 2012.


